以分子结构法解析游戏空间设计原理

作者：Luke McMillan, Nassib Azar

前言

游戏空间是游戏规则和系统运作的环境，是游戏媒介执行机制的空间。当我们谈到游戏空间的设计时，我们有时候会用纯空间的术语描述设计师在设计某种游戏空间时必须实现的东西。

在设计FPS的游戏空间时，你使用自己最喜欢的原型设计工具，画出走廊和房间，这是最糟糕的设计方法。当你用现实的规则设计游戏空间时，你会很难想出有趣的空间谜题。在写字楼似的空间里穿梭能有多少乐趣？

分子设计法是一种运用绘图理论来概念化和调整各种游戏空间类型的方法。这种理想的设计方法意味着在设计空间时，你不必思考空间本身的表现元素。本文仍然同意平面地图的重要性，但是，我们首先需要更好的工具帮我们创造这些平面空间。

本文的前半部分将介绍绘图理论中的一些实用的工具，设计师可以用于概念化各种游戏组件。本文的后半部分将检验这些工具的实际运用。借此，我们将了解到这种抽象的空间实现方法如何促进关卡的重复设计。

绘图基础

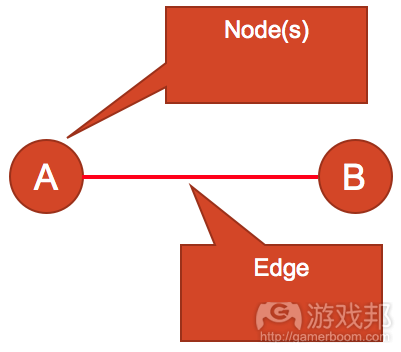
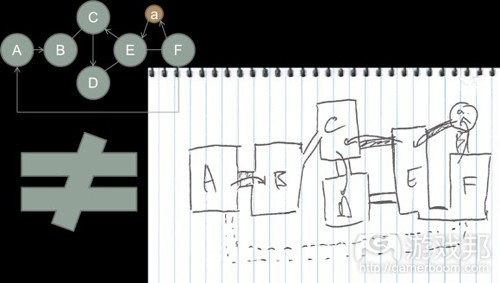
绘图理论是数学中一个宽泛而多变的领域；但是本文探讨的图形可以解释空间关系。在绘图理论中，用于解释空间关系核心概念是结点和边（图1）。结点可以表示游戏空间/房间、可拾取物品、重刷点和AI路径点。边可以定义结点之间的关系。

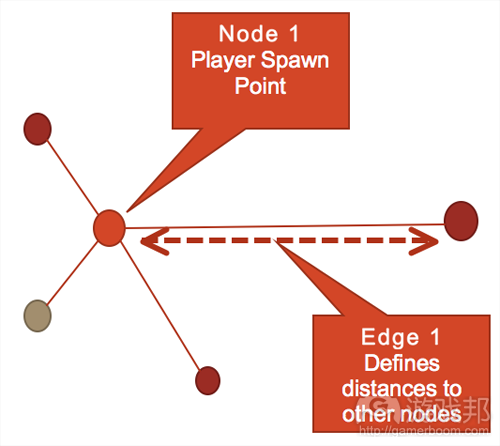
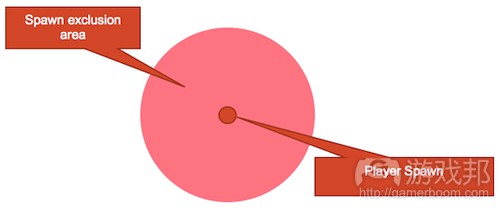
图2是一个分子结构，它是由若干个结点通过边连结起来的。在这个例子中，我们围绕玩家出现点确定了一系列标记。这就是用绘图的方法直接描述空间。结点通过边连结起来，这些边确定了玩家和其他结点之间的最短矩离。标记越大，边就应该越长。

这个方法对PVP游戏很管用。在这类游戏中，为了实现平衡，可拾取物品在空间的分布应该大致平均。重复并旋转分子结构就可以对称分布空间中的可拾取物品了。边除了确定结点之间的关系外，还可以表示关卡中的通道或其他路径。在进一步解释以前，我们先看看加粗和定向边。

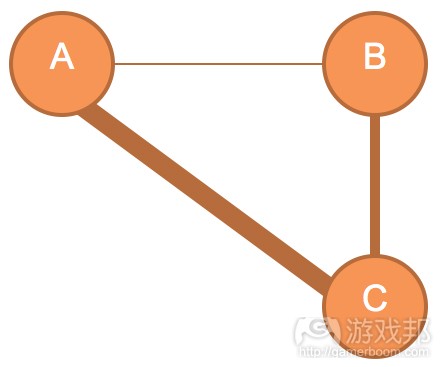
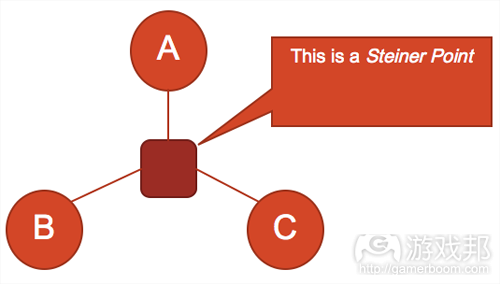
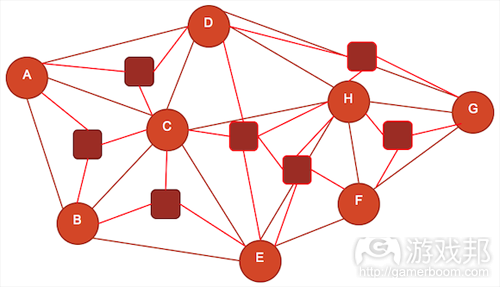
我们可以修改边的外观以表示结点之间的不同关系。在图3中，介于A与C之间的边比其他边粗。如果我们使用绘图理论设计空间，那么结点就表示某个游戏空间，那么越粗的边就表示结点之间的关系越直接，而不是表示这两个结点之间的空间更大。

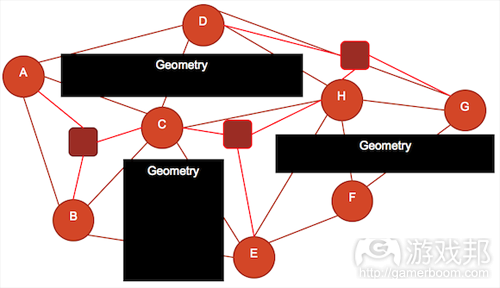
我们将图3的分子结构放到图4中，可以看出来，粗边表示的A与C之间的通道是直的，没有阻挡。相反地，A与B之间的细边表示的通道是曲折的，即更复杂。这个例子说明了，边不是描述空间的外观，而是结点之间的关系。

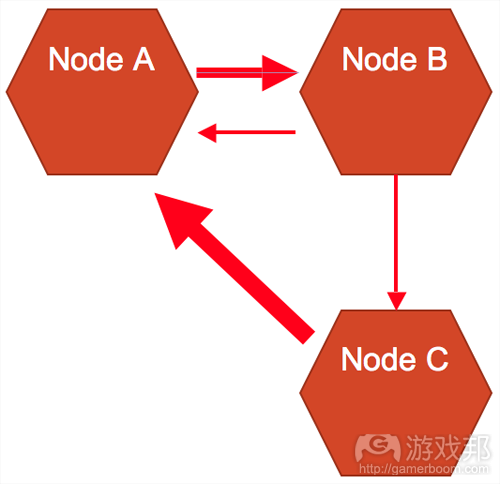
我们可以进一步丰富边所传达的信息。图5使用带箭头的边表示A与B之间的不同路径；边越粗，路径就越直接。连结B与C的是一个间接单向的出入口。连结A与C的是另一个单向的出入口。这条边更粗，表明这两个结点之间的关系更直接，曲折程度更低。

结点和边可以表示游戏关卡设计中的任何特征。例如，我们可以用边的粗细表示结点之间的通过难度。用边描述垂直空间，我们可以知道C是地图上的最高位置。还可以看出，只有通过B才能抵达C。介于B与C之间的定向边暗示，B处应该有一个“跳板”，且只能从B跳向C。对于定义特定的分子结构的关键，全凭设计师或团队的考虑。

为了进一步解释使用空间分子设计游戏空间，我们可以看以下例子。图6表示一个简单的空间分子，我们可以看出这是一个线性关卡，适用于单人游戏的地图。粗边没有出现在这个例子中，不过定向边的运用使这个空间谜题变得更有趣了。

图7告诉我们不能用空间分子做什么。使用分子的设计方法是为了将你的创意过程从纯空间理论的约束中解放出来，转而从空间关系的角度创造有趣的环境。尽管图7中的平面地图确实遵循了分子的空间关系，但它只是一个无聊的线性空间。

从空间的角度设计地图还存在其他缺陷。首先，你在平面空间中画地图，产生的一般是线性的、空间连空间的布局。当你的想象空间是二维的，你的地图也将是二维的。因此，你的地图不会产生有趣的垂直空间，更重要的是，从地图的起点看不到目标。

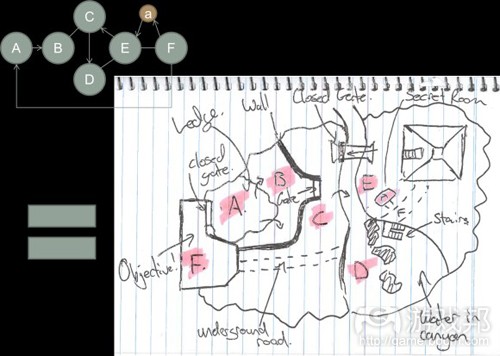
图8是相同的空间分子，但设计得更好。这个例子将各个结点作为“游戏空间”，并且用分子的边定义了这些游戏空间之间如何产生交互活动。以下是通关的假设：

在这个例子中，玩家从一个可以远眺山谷（结点A）的平台开始。除了山谷之外，还可以看到游戏区域F，一个高大的人工塔。这是最终目标，它的大小和规模立即让玩家好奇他们如何才能进入这个建筑的内部。玩家注意到，塔的入口是上锁的，但他们可以看到远处的另一个建筑，区域E中的一个大金字塔。这个金字塔有一个宏伟的入口，非常吸引玩家的注意力——它是地图上唯一让玩家有兴趣的另一个点，因此可以吸引玩家朝它走去。

在区域A的起点和金字塔之间，玩家遇到许多障碍：一堵大墙、一座大门关上的桥和一个深水峡谷。玩家有时间从他们的高台位置查看整个场景，对地形有个基本的了解。玩家从A开始计划路线。

玩家从A的高台跳下来——这是一个单向入口。在区域B，玩家必须想办法打开大门。一开始，他们会被跨越峡谷的桥所吸引，但他们很快发现桥被上锁了，并且只能从另一端打开。在桥的附近，玩家注意到有一片岩石区，他们可以从那里跳进河里，并且不会受伤。

玩家入水后，沿着河流达到一片开阔的水域。这里，玩家发现一段楼梯可以通向金字塔所在的高地。进入金字塔后，玩家看到一条地下通道连接着位于区域F的目的地。一旦玩家接近区域F，路就会从玩家身后开始崩塌，所以这是一条不归路。

隐藏的房间a将F与E连接起来，然而它也是一个单向入口，只能从E进入。一旦玩家进入房间，它就开始被大水淹没，阻断通向F的路。这样，玩家就不得不前往区域E。

区域F是目的地，玩家只有进入F才能继续前进。注意，因为区域A是单向入口，区域F被关闭，所以玩家不能返回刚才那片开阔的区域。

图9表现的是对相同分子结构图的另一个解释，这一次我们用更形像的房间来表示空间。

在这个游戏过程中，玩家从A开始，这是一个带两个门的房间，一个打开了一个关闭着。玩家从唯一打开的那个门进入另一个更大的房间B。这个房间有一个门，但是锁坏了打不开，所以玩家知道无法由此通过。在B内部有许多箱子，玩家跳上去才能离开这个房间。

在这个高大的房间上方是一个悬挂着的支架。玩家俯视这个区域可以看到一个房间E。玩家从一个箱子跳到另一个箱子，慢慢地探索垂直空间。当他达到最高位置时，就进入一个小隧道（C），然后逐渐下降。

穿过隧道后，玩家来到户外区域D。在这里，他可以通过楼梯从D到达E。进入E后，玩家可以穿过之前看到的桥。在去F的路上，玩家发现一个可拾取物品，就位于他之前在B达不到的箱子上。如果他决定跳回那个箱子，那么他就必须依次返回B、C、和D。

图8和图9表明，利用分子设计一个平面地图是一个设计创意空间的好办法。这种概念化的方法迫使设计师在关卡设计的平面地图阶段时必须安排有趣的空间选项。根据我自己的经验，用平面地图设计出来的关卡通常是很无趣的、线性的——这是用纯2D空间创造法制作有趣的3D空间的结果。

更先进的工具

既然我们已经探讨了绘图理论的基本原理，现在就可以探讨一下设计师们设计游戏空间时使用的一些工具。注意，这些工具只是设计师可以使用的一些概念。因为本文挪用了一些想法，所以有些例子必须脱离对这些概念的纯数学解释。本文将探索的绘图概念如下：

*支配理论

*斯坦纳点

*生成树

领土/控制理论

领土理论可以帮助我们理解结点如何产生作用区域（AOE）和这个AOE如何覆盖其他结点。对于从玩家体验的角度解释现存的地图，这是一个特别实用的理论。在这种方法中，各个结点代表“游戏区域”和这个空间的游戏强度。

“游戏区域”这个概念，最初是在设计《半条命》时用于研究和指代“体验密度”的。体验密度是由Valve的设计师们在开发《半条命》时杜撰的。这个概念是指基于距离而非时间的游戏体验。这个基本概念是，玩家应该总是自主选择游戏体验的下一个区域。在玩家来到高密度的区域前，设计师应该给玩家足够多的时间收集掉落物品或单纯地探索地图。

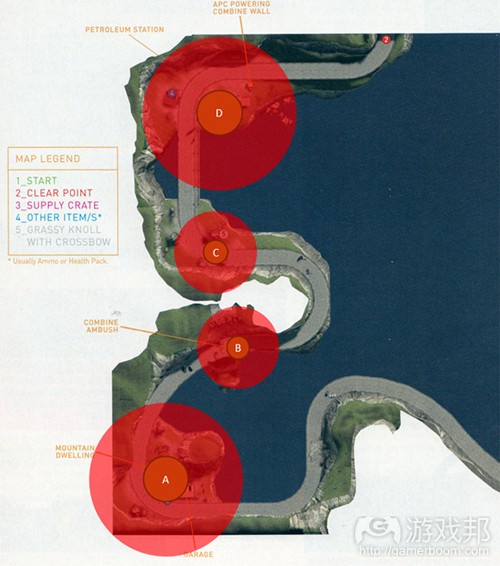
图10是取自《半条命2》的一段地图，从中我们可以看出如何使用领土理论增加体验密度。在这张地图中，我们有三个明显的高密度区域，分别用A、B和C表示。各结点的AOE分别表示各区域的游戏密度。AOE越大，玩家面临的挑战就越大。

如果我们在设计时采用领土理论，那么我们就能使用领土来确保我们不会强迫玩家进入连续的、高密度的游戏区域。也就是说，我们希望用分子设计来确保在不同区域之间，玩家有足够的情绪“冷却”时间。我认为这些冷却区域类似于音乐的动态。在《The Clarinet and Clarinet Playing》一书中，音乐家和作者David Pino将这个概念总结如下：

这么思考：如果你站在海滨眺望一片宽广的大海，你可能会觉得无聊。但是，如果海面上漂着一支小船，你就会觉得大海很有生机，很迷人。类似地，如果你的视野突然被上百只船充满，没有哪一支船会让你留意很久。相同的原则也适用于音乐演出：如果听众体会不到旋律中的微秒变化，他们就会觉得沉闷；但如果除了微妙变化，他体会不到其他东西，他们也仍然觉得无趣……音乐中最重要的元素是它的韵律起伏流动。

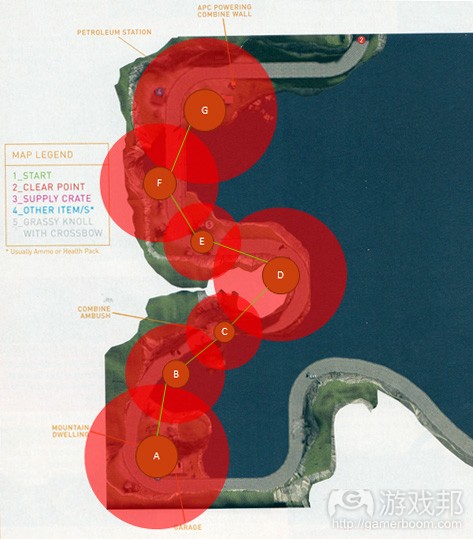
为了更好地解释领土理论的作用方式，我们可以使用取自《半条命2》中的相同例子，但我要刻意破坏体验密度（图11）。在图11中，覆盖的游戏区域用重叠的红色AOE表示。从玩家体验的角度看，这就像阅读一本不带标点的书。游戏体验缺少情绪状态的混合，因为玩家“除了微妙变化，他体会不到其他东西了”——用Pino的话说。

为了解决体验密度的问题，我们可以在这张地图上运用领土理论。取决你希望玩家有多少冷却空间，你可以调整“支配重叠”来适应冷却空间。例如，你可以将分子中的重叠结点移除，这样就没有覆盖区域了（如图10）或者你可以修改游戏区域，这样游戏密度就会降低，但是更加频繁（如图12）

从关卡概念化的角度看，领土也可以用于定义“刷出排斥区域”或任何其他类型的“排斥区域”。所谓的排斥区域就是指，在某个区域内某物不允许出现——即另一个结点的领土区域内不允许与其他结点的领土区域重叠。在使用领土理论时，点可以表示可拾取物品或玩家刷出点。因此，红色的AOE就形象地表示事件刷出范围的最小距离。

图13是一个使用领土确定排斥区域的例子。结点代表一个玩家刷出位置，也可以表示其他物品刷出点。这个围绕在结点周围的红色AOE形像地代表另一个刷出可以出现的最小范围。例如，如果我们遵循虚幻开发工具包（UDK）的限制，那么我们可能说根据我们的地图大小，处在相同垂直空间的各个刷出点必须彼此相距至少1024UU。你的领土区域的规则是灵活的；然而，对于这个例子，这个规则是，在这个领土区域内不允许出现其他刷出活动——至少从平面的角度看。

图14是一个必须解决的领土问题。这个问题可能是因为重叠刷出或可拾取物品太接近。为了移除重叠部分，我们可以把这些结点分得更开一些，或者简单地使用关卡地形来缓和重叠问题，如图15所示。

但是，当运用领土理论时，你应该有一点常识。一旦你添加上关卡地形，你的设计就会更加复杂，这需要你修改某些规则。

在图16的例子中，我使用刷出的排斥系统在一个不对称环境中分布刷出位置。注意，我有意将刷出位置3远离刷出位置1和2。

这么做的原因是，刷出位置1和2的接近向量更少——即在玩家的视域内可以看到任何接近的敌人。而刷出点3的接近向量的弧度很大，玩家的视域不可能覆盖到整个范围，因此必须将这个点与其他点的距离拉大，以弥补这个劣势。

你可以将这个相同的排斥系统运用于其他可拾取物品——可拾取物品越强大，刷出排斥范围就越大。但正如前面提到的，关卡地形和其他因素如可拾取物品和玩家在游戏空间中移动的能力必然要求使用更复杂的分析工具——也就是生成树和斯坦纳点。

使用绘图理论理解玩家的选择和策略

所有游戏关卡都提供空间谜题。这些谜题的形式有很多，运用绘图理论可以改进某些与最佳行动策略有关的谜题，这类谜题经常出现在死斗模式的地图中。

玩家的游戏体验有赖于大量选择；但是，过多的选择与毫无选择一样糟糕。进一步说，玩家通过执行“好”策略选择而得到胜利时，会产生强烈的自豪感。到目前为止，我们已经使用绘图理论解释了游戏空间的结构，；但绘图理论的实用性不仅仅体现这一方面，还体现在考察以人为诡计和策略为主要关切点的关卡设计。我们将结合斯坦纳点和生成树，以及最大化和最小化通道的原理，来理解这些人为因素。

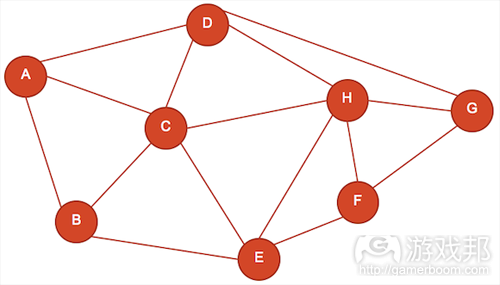
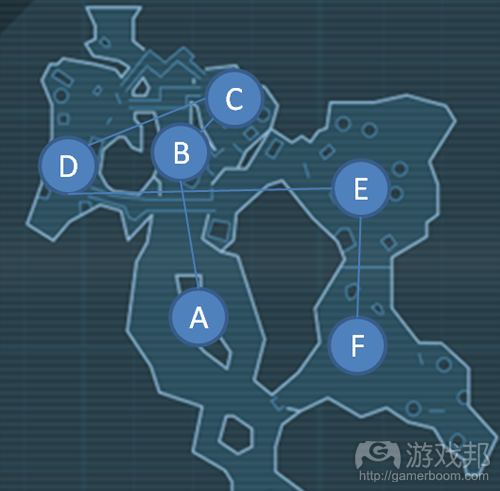
图17是一个假想关卡的例子。结点A-E分别表示不同类型的游戏空间，各条边表示玩家从一个空间移动到另一个空间的可用路线。注意，边并不表示通道，而是玩家的选择路径。边的长短是根据路线的复杂程度确定的——也就是，边越长，通过这条路线的时间就越长。在图17中，各个空间（结点）都给玩家提供3到5个不同的选择。从这张图还可以看出，玩家要穿过整个地图需要怎么走。

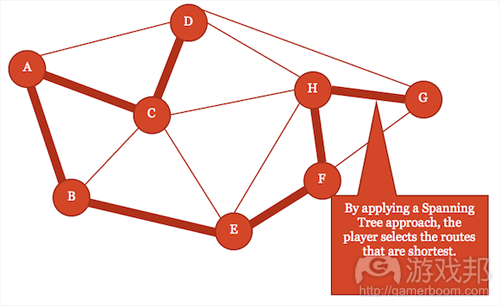
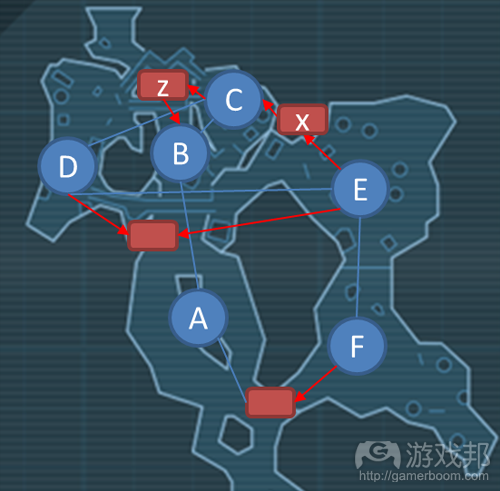
生成树可以用来寻找结点之间的最佳连接点。我们还可以借助这个工具理解玩家在这个地图上的行为，以及寻找设计不公平或不平衡的方面。如图18所示，我们可以这样使用生成树分布可拾取物品、确定刷出点和放置关卡地形，以抵消任何明显过强的行为策略——可能出现在PVP地图中。

尽管制定关卡的最佳行动策略的确切排列是定义游戏空间的好办法，但我们必须进一步考虑玩家可能想到的诡计和突发事件。比如，玩家走捷径。捷径是指规则之外的一系列策略选择。玩家在任何游戏环境中都会寻找走捷径的机会，一旦他们发现到捷径就会感到非常满足。我们可以通过斯坦纳点理解这种行为。

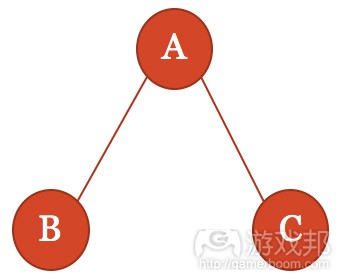
寻找斯坦纳点就是寻找连接多个结点的最短边的连接点。Raph Koster在他的“游戏数学”的演讲上提到一个例子，可以帮助我们理解如何在游戏中运用斯坦纳点。在他的展示中，Koster表示“如果有三个结点，你要在它们之间创造尽可能最短的路线，那么你需要多少条最短路线？”Koster提出大多数人会做出类似图19的回答。

这个问题的答案有一点儿偏了，因为它需要另一个结点——斯坦纳点。我们在图20中加入斯坦纳点，这样就得到这个问题的最佳解决方案了。我们可以像看待其他图一样看待斯坦纳点及其所创造的边。在游戏中，我们可以用加粗的定向边帮助确定斯坦纳点如何成为地图上的一个高度元素或另一个单向入口，如传送门或起跳台。

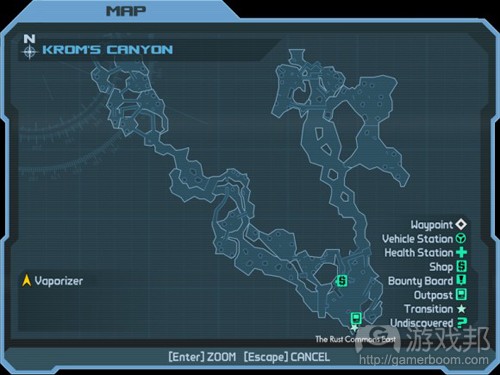
斯坦纳点就是一种捷径。它是玩家在探索地图时会找到的一个关卡设计元素。关卡设计师的秘密就是让斯坦纳点在地图上表现得比生成树路线还隐蔽。游戏《边境之地》就是一个好例子。在下图的地图中，大部分的生成树路径是很明确的，表现为清楚的路径和跳台。

斯坦纳点以高度元素的形式存在于这款游戏中，当玩家跳到地图中的某个部分时，也就是跳过生成树的大部分路线，这样就省去了许多路程。《边境之地》的克罗姆峡谷就是这样一个例子：玩家可以从上升的平台跳下来，快速移动到地图上的另一个地方，从而创造一个斯坦纳点（如图21）。

图22（取自克罗姆峡谷）表现的是如何在关卡设计中运用生成树和斯坦纳点。在这个例子中，玩家为了从结点A到结点F，必须设计一个生成树方案。这种关系通过一系列渐渐上升的、与桥相连的平台体现在关卡设计中。在部分地图中，许多物品分布也使用了斯坦纳点。

我在图23中添加了两个斯坦纳点。不过，在这个空间分子中其实还有其他斯坦纳点，这些点表示放置在高台上的可拾取物品，只有通过物品上方的结点才能得到。所以，这些结点不仅作为捷径与斯坦纳点相连，还是玩家探索作为空间谜题的地图时的收益获得位置。

图24将这个部分拓展为一个更确切的分子，并添加了另外两个斯坦纳结点，以体现玩家在上升或下降时如何探索这个空间。

现在我们已经知道斯坦纳点如何从空间谜题的水平上发生作用，现在我们可以回顾一下在图17中引入的生成树分子。如果我们将斯坦纳点运用于连接就近范围的结点，那么我们就会得到类似图25的结果。

这些斯坦纳结点具有多种形式。它们可以作为传送门、关卡地形或甚至是允许快速探索路径的高度元素。图25显示了我们在这个空间设计时可能使用到多少斯坦纳点。根据Koster的说法，太多斯坦纳点对玩家是有害的，因为玩家的选择太多了；也意味着玩家无法执行我所谓的“技术性策略”。基本上，即使玩家能够在这种地图中发现捷径，他们也不会感到有趣，因为捷径太多了。

如果我们使用关卡地形减少可能的斯坦纳点，我们就对玩家的要求就更高了。通过给予他们更少的选择（如图26），我们要求玩家执行比地图上的其他玩家的更好的策略。这么做的优点是，能在这种环境下执行更好策略的玩家会得到更大的满足感，因为他们意识到缺少选择意味着他们解决了更复杂的问题。为了说明斯坦纳点的减少如何影响难度的增加，我们只要看看下面这个取自《辐射3》的例子——图27的右下角部分。

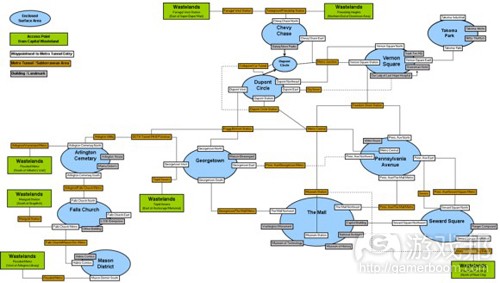
在《辐射3》中的前期部分，空间探索问题可以通过简单的生成树解决，即寻找其中的斯坦纳点。这在Vault的南部区域表显得最明显，因为这是地图的第一部分（最东的），也是玩家最想探索的部分。不过，随着难度增加，这些斯坦纳点就大大减少了；这可以从DC地铁系统中看出来，《辐射3》的主线任务的玩家遭遇战就发生在这里。

实际运用

到现在为止，我们已经了解了绘图理论的基本原理和分析了在许多商业案例中的运用，但绘图理论到底如何作为工具用于概念化游戏空间？以下是由Nassib Azar提供的分子设计法的实际运用的案例。

在这个案例中，Nassib测试、执行和提炼了分子概念，以便创造一个平衡的、多人空间，这个空间尽管简单，但玩家能探索到足够多的有趣策略。

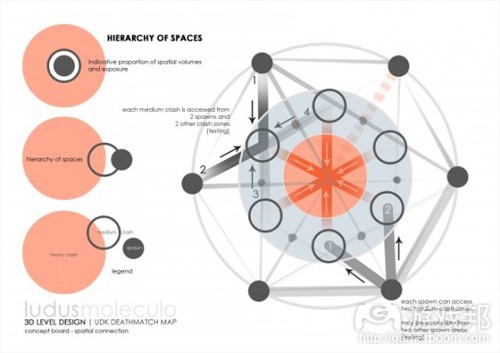
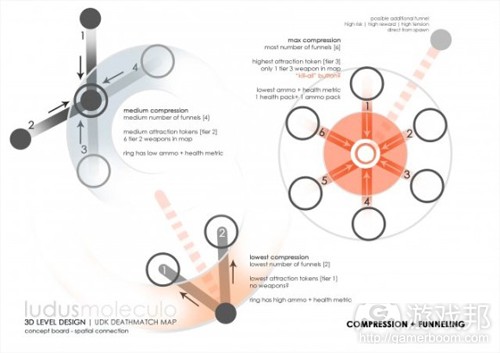
Nassib的目的是设计一个有三层体验的地图，这三层体验以三个同心圆表示。游戏空间是死斗模式地图，使用UDK默认游戏类型。外层是由低密度区域组成的，作用是“引诱”玩家进入游戏空间的最内层。

出于这个设计的目的，Nassib用玩家积极尝试杀死对方的次数衡量“密度”。图28是这个地图的草图。这张图显示了瓶颈点、交集点、刷出点和可拾取武器点，当玩家接近地图的中心时，这些点可以用来增加游戏体验的密度。

经过一些初期纸上原型和反馈后，三个不同密度的中心游戏空间的核心想法最终变成一个更具体的分子结构，从而确定空间。图29是早期概念的重制图。在这张图中，我们仍然有相同的一组同心圆表示游戏的密度，但是添加了边，以体现外层如何引导玩家进入中层。

为了达到这个目标，Nassib运用了“浓缩和漏斗”的概念，这种工具可以说明如何迫使游戏空间中的玩家使用各种可以提升情绪状态的游戏元素。在图29中，各个边代表示导向结点的额外的压迫向量。在这个例子中，结点表示用于战斗的空间；导向结点的边越多，这个结点的压迫程度就越高（结果是，游戏体验的密度也更高）。结点大小表示压迫程度的增加，进而增加游戏的密度。

即使运用分子设计意味着区别游戏体验和关卡地形，Nassib还是选择研究纯地形的空间表现法是否具有内在的玩家体验价值。Nassib的分子原型的六边型属性值得进一步探究。问题是：分子结构转变成真实的关卡地形后仍然保有原来的设计意图吗？

这个用于定义整个游戏空间的原型分子以灰盒关卡的形式用UDK反复重制。显然，经过原型制作，这个尝试确实有优点；玩家体验的密度随着玩家逼近地图的中心而增加。结点变成通用的游戏空间，而边变成引导玩家进入这些空间的通道。

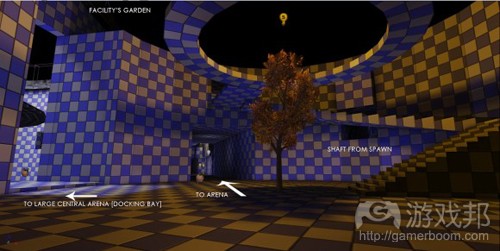
图30是灰盒的改良版本。从图上可以看出来，原始分子转变成可游戏的空间。在测试时发现，空间大小必须增加，才能适应游戏密度的增加。

空间大小是根据理想的游戏密度的最佳空间大小而确定的。原始分子设计在这方面转换得很好。游戏空间随着玩家向地图中心移动而渐渐增大，然而这个区域又很小，足以迫使玩家采取近战策略，从而增加游戏密度。

为了增加地图中心对玩家的吸引力，必须合理分布各种可拾取武器。用于确定可拾取物品位置的分子主要有两种：可拾取武器可以让玩家更快向地图的中心移动。可拾取的药水会吸引玩家探索各个游戏区域的周边环境。设置这两种性质不同的不仅增加了进攻和防御玩法的不同行动策略，而且有助于将游戏活动平均地分配到整个地图中，而不只是集中在最中心的地区。

图31进一步分解了图30。在中间结点（上左边）的附近，区分了导向它的两类不同的边。边1和边2来自刷出点，而边3和边4来自其他中间结点。这意味着不同的危险程度，因此要由不同的边表示。尽管最初设计假想表明，边1、边2和边3、边4之间存在某类可识别的差异，灰盒几经修改才观察到这个假想的真实样貌，见图32。

从这个灰盒的早期重制版可以看出设计存在根本的缺陷。尽管随着玩家逼近地图中心，游戏密度增加了，并且第二层机制也出现了，但玩家越来越觉得自己只要在地图外圈就能得到很多好处，打到无数刷出的敌人。测试的结果表明，边1和边2上升成为单向入口，可以吸引玩家进入地图，同时防止已经在地图内的玩家进入刷出点。升高的走廊被重新概念化为物理空间，如图33所示。

分子设计法还有利于可拾取物品的分布，物品放置遵循类似关卡地形的对称分布。尽管对称分布减少了地图设计的工作量，但过多的对称通常是很无聊的，甚至让玩家感到困惑。

为了解决这个问题，应该用不对称作为玩家探索、分布着不同类型武器的房间和游戏机制的标志。使各个房间的布局不同有两个目的：一是帮助玩家探索各个房间，并“感知”各个房间的优势。如果玩家感到不公平，那么无论系统本身多么公平和平衡，玩家也会被他们认为有漏洞的元素所吸引，即使实际上这些元素并没有漏洞。

事实上，第二圈的房间各自包含不同类型的空间分子。这些分子的差异通过不同的阻塞点和掩蔽元素体现出来。从图34和图35中的对比中可以看出这种结果；两张图的房间都在第二圈，各自提供不同类型的游戏体验。

再次重制和测试后，发现玩家更可能进入主要的房间，而不是第二圈/中间房间，但没有达到预期的比例。在中心房间的游戏体验的密度必须非常高，但是要达到理想的体验，玩家流量还不够。当然，这可以通过缩小空间来解决，然而因为关卡美术的大部分已经进入制作阶段，所以有必要寻找替代选择。

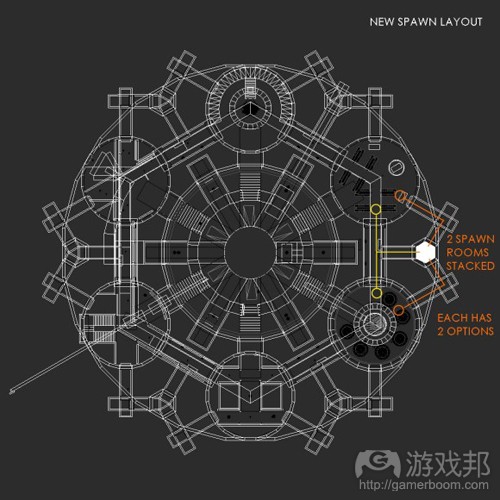
为了最大化体验，使玩家刷出点的第二圈出现在第二圈的夹层中。从更上面的刷出点走到中心房间的距离比从地面层的更短，因此会大大增加中心房间的流量，从而达到理想的效果。

与中间房间相比，图36中的两个重叠的刷出点没有相同的“从刷出到沉浸”的时间。换句话说，上面的边与下面的边并不相等，而其实它们应该相等。修改分子设计来改变刷出点的位置，“从刷出到沉浸”的时间差异与之前的刷出点的相比，就可以忽略不计了。

对称分子使地图上的楼梯和电梯分布更公平；然而，在实际设计中，三个电梯的分布被有意区别开来（图37）。这个方法的基本原理是，突出感知不公平的心理状态。测试表明，大多数玩家认为靠近刷出点的楼梯更有优势，这种优势不会被用来反对他们。梯楼本身的设计是不对称的，这么做的作用有两个：一是帮助玩家探索，二是丰富中间房间的游戏体验。

另一个用于实现平衡的策略并非出自绘图理论本身，但突出了绘图理论如何帮助解读玩家行为。Kismet脚本会使游戏每过三分钟比较一次分别经过这六个中间房间的玩家的数量，然后确定哪个房间的流量最少。活动量最少的房间就要增加一个触发器。

当玩家激活触发器时，它就会将另一个玩家放入这个空间，玩家互杀完毕后计算击杀数目。（图38是这张地图的俯视图，也就是玩家死前看到的最后一个场景）这有助于增加流量最少的房间的游戏密度，从而通过机制而不是静态绘图创造一个动态平衡的系统。当出现这个场景时，玩家可以选择使用斯坦纳点的方案来解决空间问题——也就是达到目标的最短路线。

一旦脚本确定最少流量的房间，这个地图上的所有玩家就会收到声音和文字通告，让人们知道哪一个中间房间的触发器可以使用了。取决于玩家的当前位置，他们面临两个选择。他们可以通过最短最危险的路径达到中心房间，或者，他们也可以选择通过中间房间的更长但更安全的路径，从而避开中心的冲突区域。

这么做，我们就为玩家创造了两种不同的策略；他们可以使用中间房间作为斯坦纳点或使用外层房间作为生成树（图39）。这些策略性的选项是为了激发玩家的成就感。玩家会感到骄傲是因为他们觉得走捷径达到合适的房间，这是以智取胜的表现。填充在各个房间的关卡资源也起到减少斯坦纳点总数的作用，从而提高找到有限的解决方案的内在价值。

最后一张地图经过了8次大修改，既升级了灰盒，也调整了分子结构才变成现在这个样子。每一次修改都以修正后的分子概念为基础，之后才转变成灰盒。所以，各次修改都有明确的目标，这极大地增强了最终成果的效果，特别是考虑到时间非常有限。

结论

Dan Cook和Chris Crawford等人研究了人们玩游戏的动机，启发我们产生学习和改进这些新技术的想法。Raph Koster进一步细化这个概念；人类是寻找模式的机器，当我们在游戏中识别并学会它的模式时，我们就能从游戏中收获快乐。因此，基于模式的分子设计法来定义游戏空间直接迎合了人类天性，的确有实用价值。

另外要记住的一点是，玩家不会把游戏当作平面地图，他们是在自己的视域中感知地图。因此，你希望执行的分子的规模和“可识别度”受制于玩家在任何时候可以感知到的游戏世界。

设计师经常制作迷宫类地图，尽管这种地图从平面角度很容易理解，但通过玩家有限的视角，是绝对无法全整探索的。所以，为了让玩家觉得地图有趣，分子和模式不一定要非常复杂。

相反地，设计良好的游戏空间往往有许多嵌套分子，而不是一个分子就定义了整个游戏空间。从绘图理论的角度看，Nassib Azar制作的实例是比较简单的，但动态游戏元素产生的分子排列的数量为玩家提供了一系列多样而可控制的策略。

值得一提的是，使用绘图理论概念化和分析游戏空间并不是什么新思路，事实上很多人都以各种形式讨论了这个想法。这个研究的灵感最初来源于Raph Koster和他的“游戏数学”展示。我向所有对设计感兴趣的人推荐他的工作。Joris Dormans也写了一些与绘图理论相关的文章，关卡设计师可以当作参考。Dormans的《Adventures in Level Design》和《Level Design as Model Transformation》都很不错，清楚地说明了这个工具的广泛用途。

（本文为游戏邦/gamerboom.com编译）